Editors’ note: We inadvertently published part 2 of the “Statistics in the Literature” (May 2006, p. 15) series installments in May (p. 15) out of order. In fact, the following series installment should have preceded the installment we published in May. Therefore, the following series installment is the last in the EBM series. We apologize for any inconvenience.
Why Do Statistical Methods Matter?
Critical appraisal of the literature does not stop with evaluation of bias and review of results. While it would be nice to simply trust that the reported methods in a paper tell the whole story, this approach would be inconsistent with the core principle of EBM: a global attitude of enlightened skepticism. Statistics in the literature should be subject to the same appraisal as every other aspect of a study.
But is such detail truly necessary? If a paper meets the standard criteria for validity, can’t we assume that the statistics are also valid? Most of us would like to be able to just accept that the P values and confidence intervals we see in a paper are appropriate. Even EBM experts tend to feel this way, as evidenced by the statement in Sackett, et al. (1998) that “if good [study] methods were used, the investigators probably went to the effort to use good statistics.” Unfortunately, repeated studies of the statistical methods reported in literature across many fields suggest that up to 50% of papers contain major statistical flaws, many of which could affect the conclusions of the paper. This occurs even in top-tier journals, so no source is immune.
This problem is compounded by the fact that the statistical knowledge of the average clinician is quite limited. Journals certainly have a responsibility to ensure the presentation of valid research, but how many of us (as reader or reviewer) are qualified to assess the statistical methodology from which a study’s conclusions result? It’s trouble enough to work through the critical appraisal process outlined in the previous installments of this series, let alone dig deeper into how the results were generated.
In fact each reader must act as his or her own judge of a study’s ultimate value, and ignorance of basic statistical principles cannot be an excuse for accepting faulty research. Remember, we make patient care decisions based on our reviews of the literature, so there is a very real incentive to ensure we apply the best evidence both epidemiologically and statistically: Our patients are counting on us. With this in mind, we will conclude this series with a two-part discussion of some of the core statistical concepts to consider when evaluating a paper.
Commonly Reported Statistical Terms
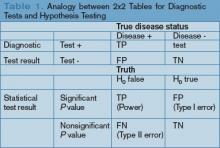
P values: The P value is perhaps the most widely reported yet least understood statistical measure. Consider a comparison of a new treatment with placebo: The null hypothesis (H0) is the hypothesis of null effect, usually meaning that the treatment effect equals the placebo effect. The technical definition of a P value is the probability of observing at least as extreme a result as that found in your study if this null hypothesis were true. The condition in italics is crucial: Remember, we never know if the null hypothesis is true (and if we did, there would be no need for further research).
Usually, however, the P value is interpreted incorrectly as the probability that a study’s results could have occurred due to chance alone, with no mention of the condition. Thus, a P value of 0.05 is thought (wrongly) to mean that there is a 5% chance that the study’s results are wrong.